什么是二次规划(Quadratic Programming)?
二次规划是一种用于优化多变量二次函数的方法,该函数可能是线性约束的,也可能不是。许多现实世界中的问题,例如优化公司的投资组合或降低制造商的成本,可以用一个二次规划来描述。如果目标函数是凸的,则可能存在一个可行解...
二次规划是一种用于优化多变量二次函数的方法,该函数可能是线性约束的,也可能不是。许多现实世界中的问题,例如优化公司的投资组合或降低制造商的成本,可以用一个二次规划来描述。如果目标函数是凸的,则可能存在一个可行解,并且可以用已知的算法(如扩展单纯形算法)来求解。存在一些非凸二次函数的方法,但这些方法复杂且不易获得。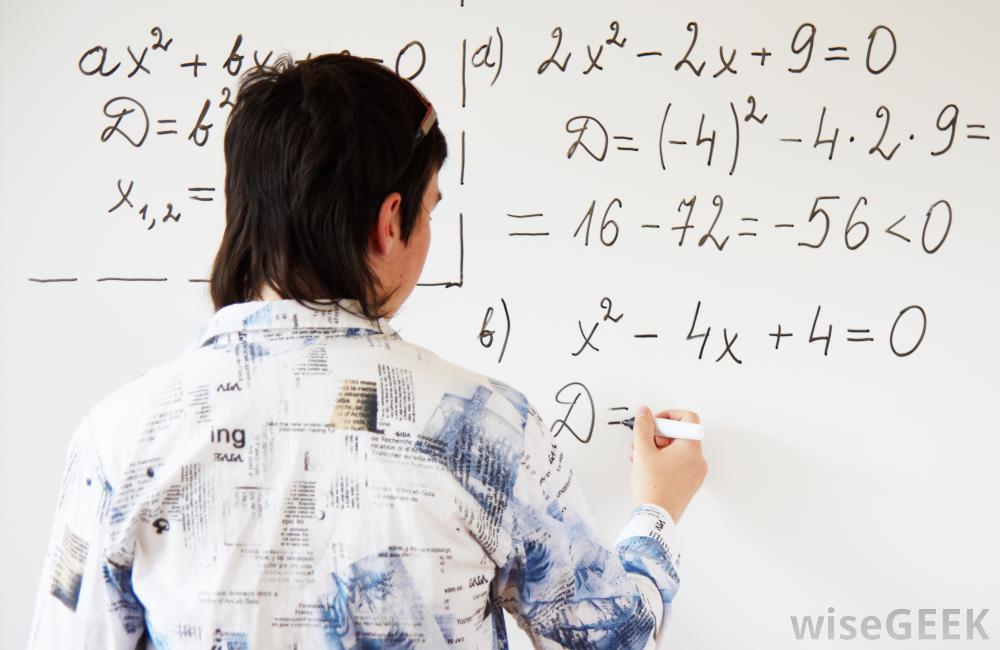 二次型方程可用于二次规划。数学优化技术用于二次规划以最小化目标函数。目标函数由许多可能有界或无界的决策变量组成。决策变量的幂为0、1或2。目标函数可以一个二次规划的例子是:最小化f(x,y)=x23y2-12y12,其中x y=6,x>;0和y≥0。用多元二次函数来描述现实世界中的问题是很有趣的,运用现代投资组合理论,金融分析师试图通过选择与给定预期收益相关的风险最小化的资产比例来优化公司的投资组合,由资产权重和资产之间的相关性组成的二次方程描述了可以使用二次型最小化的投资组合方差另一个例子可能是一个制造商用一个二次方程来描述不同质量成分和产品成本之间的关系制造商可以通过在二次规划中加入线性约束,在保持一定标准的前提下使成本最小化。求解二次规划最重要的条件之一是目标方程的凸性,二次函数的凸性由Hessian或其第二次函数的矩阵决定导数,当Hessian矩阵为正定或半正定时,即所有特征值分别为正或非负时,称为凸函数;如果Hessian矩阵为正且存在可行解,那么局部最小值是唯一的,并且是全局最小值。如果Hessian是半正的,可行解可能不唯一。非凸二次函数可能有局部或全局最小值,但它们更难确定。用二次规划来求解凸二次函数有很多种方法,其中大多数是常用的方法是单纯形算法的扩展。其他一些方法包括内点或障碍法、主动集方法和共轭梯度法。这些方法被集成到某些程序中,如Mathematica®和Matlab®中,它们可用于许多编程语言的库中。
二次型方程可用于二次规划。数学优化技术用于二次规划以最小化目标函数。目标函数由许多可能有界或无界的决策变量组成。决策变量的幂为0、1或2。目标函数可以一个二次规划的例子是:最小化f(x,y)=x23y2-12y12,其中x y=6,x>;0和y≥0。用多元二次函数来描述现实世界中的问题是很有趣的,运用现代投资组合理论,金融分析师试图通过选择与给定预期收益相关的风险最小化的资产比例来优化公司的投资组合,由资产权重和资产之间的相关性组成的二次方程描述了可以使用二次型最小化的投资组合方差另一个例子可能是一个制造商用一个二次方程来描述不同质量成分和产品成本之间的关系制造商可以通过在二次规划中加入线性约束,在保持一定标准的前提下使成本最小化。求解二次规划最重要的条件之一是目标方程的凸性,二次函数的凸性由Hessian或其第二次函数的矩阵决定导数,当Hessian矩阵为正定或半正定时,即所有特征值分别为正或非负时,称为凸函数;如果Hessian矩阵为正且存在可行解,那么局部最小值是唯一的,并且是全局最小值。如果Hessian是半正的,可行解可能不唯一。非凸二次函数可能有局部或全局最小值,但它们更难确定。用二次规划来求解凸二次函数有很多种方法,其中大多数是常用的方法是单纯形算法的扩展。其他一些方法包括内点或障碍法、主动集方法和共轭梯度法。这些方法被集成到某些程序中,如Mathematica®和Matlab®中,它们可用于许多编程语言的库中。
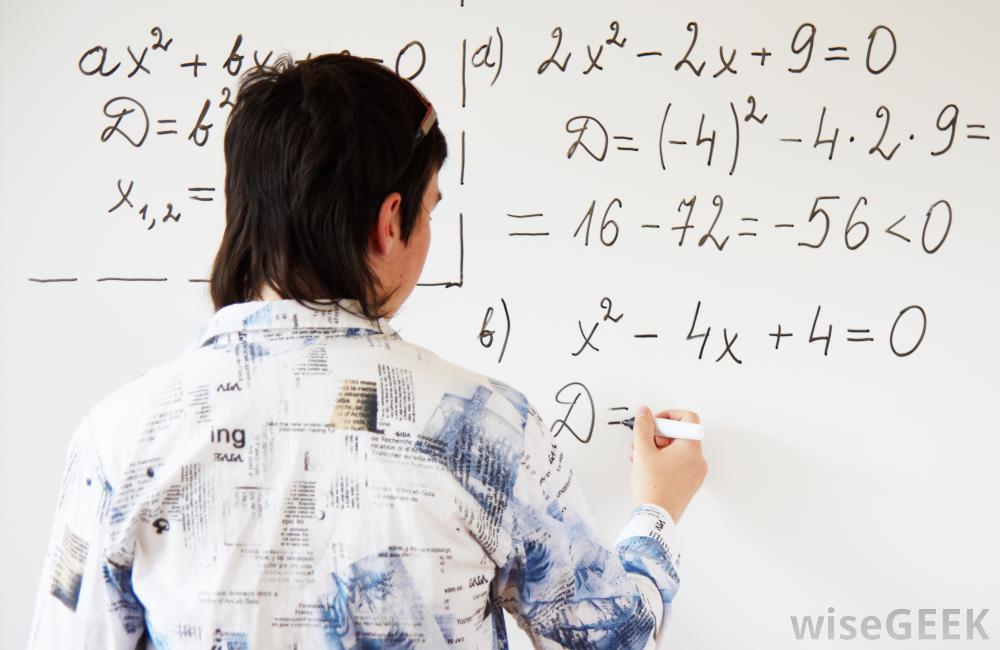 二次型方程可用于二次规划。数学优化技术用于二次规划以最小化目标函数。目标函数由许多可能有界或无界的决策变量组成。决策变量的幂为0、1或2。目标函数可以一个二次规划的例子是:最小化f(x,y)=x23y2-12y12,其中x y=6,x>;0和y≥0。用多元二次函数来描述现实世界中的问题是很有趣的,运用现代投资组合理论,金融分析师试图通过选择与给定预期收益相关的风险最小化的资产比例来优化公司的投资组合,由资产权重和资产之间的相关性组成的二次方程描述了可以使用二次型最小化的投资组合方差另一个例子可能是一个制造商用一个二次方程来描述不同质量成分和产品成本之间的关系制造商可以通过在二次规划中加入线性约束,在保持一定标准的前提下使成本最小化。求解二次规划最重要的条件之一是目标方程的凸性,二次函数的凸性由Hessian或其第二次函数的矩阵决定导数,当Hessian矩阵为正定或半正定时,即所有特征值分别为正或非负时,称为凸函数;如果Hessian矩阵为正且存在可行解,那么局部最小值是唯一的,并且是全局最小值。如果Hessian是半正的,可行解可能不唯一。非凸二次函数可能有局部或全局最小值,但它们更难确定。用二次规划来求解凸二次函数有很多种方法,其中大多数是常用的方法是单纯形算法的扩展。其他一些方法包括内点或障碍法、主动集方法和共轭梯度法。这些方法被集成到某些程序中,如Mathematica®和Matlab®中,它们可用于许多编程语言的库中。
二次型方程可用于二次规划。数学优化技术用于二次规划以最小化目标函数。目标函数由许多可能有界或无界的决策变量组成。决策变量的幂为0、1或2。目标函数可以一个二次规划的例子是:最小化f(x,y)=x23y2-12y12,其中x y=6,x>;0和y≥0。用多元二次函数来描述现实世界中的问题是很有趣的,运用现代投资组合理论,金融分析师试图通过选择与给定预期收益相关的风险最小化的资产比例来优化公司的投资组合,由资产权重和资产之间的相关性组成的二次方程描述了可以使用二次型最小化的投资组合方差另一个例子可能是一个制造商用一个二次方程来描述不同质量成分和产品成本之间的关系制造商可以通过在二次规划中加入线性约束,在保持一定标准的前提下使成本最小化。求解二次规划最重要的条件之一是目标方程的凸性,二次函数的凸性由Hessian或其第二次函数的矩阵决定导数,当Hessian矩阵为正定或半正定时,即所有特征值分别为正或非负时,称为凸函数;如果Hessian矩阵为正且存在可行解,那么局部最小值是唯一的,并且是全局最小值。如果Hessian是半正的,可行解可能不唯一。非凸二次函数可能有局部或全局最小值,但它们更难确定。用二次规划来求解凸二次函数有很多种方法,其中大多数是常用的方法是单纯形算法的扩展。其他一些方法包括内点或障碍法、主动集方法和共轭梯度法。这些方法被集成到某些程序中,如Mathematica®和Matlab®中,它们可用于许多编程语言的库中。
- 发表于 2020-09-04 14:17
- 阅读 ( 2491 )
- 分类:其他类型
你可能感兴趣的文章
- 什么是临时投票(Provisional Ballot)? 1057 浏览
- 光明节布什是什么(Hanukkah Bush)? 765 浏览
- 什么是拍卖(Auction Sales)? 734 浏览
- 你在工作中不应该讨论哪些话题(Some Topics That You Should Not Discuss at Work)? 789 浏览
- 星座狮子座的性格特征是什么(Personality Characteristics Associated with the Astrological Sign Leo)? 1143 浏览
- 当我向慈善机构捐款时,我应该考虑什么(What Should I Consider When Donating to a Charity)? 1350 浏览
- 什么是乳胶奶嘴(Latex Pacifiers)? 713 浏览
- 什么是高空炸弹(Lob Bomb)? 836 浏览
- 我在二手商店能找到什么(What can I Find at a Second Hand Store)? 634 浏览
- 什么是字母块(Alphabet Blocks)? 1122 浏览
- 什么是诱饵陷阱(Booby Trap)? 1077 浏览
- 什么是战斧(Tomahawk)? 1367 浏览
- 波曼德是什么(Pomander)? 1120 浏览
- 什么是香榭剑(Shamshir Sword)? 749 浏览
- 什么是手相术(Palmistry)? 768 浏览
- 基础学习技能有哪些(Different Types of Elementary Study Skills)? 808 浏览
- 什么是卡姆内西亚(Camnesia)? 632 浏览
- 教诗歌最好的方法是什么(Best Tips for Teaching Poetry)? 838 浏览
- 写草书应该知道些什么(What Should I Know About Writing Cursive)? 596 浏览
- 什么是婚礼祝酒(Wedding Toasts)? 886 浏览
- 什么是修道会(Prosection)? 889 浏览
- 什么是圣周(Holy Week)? 2216 浏览
- 什么是PSAT测试(PSAT Testing)? 936 浏览
- 什么是维多利亚十字架(Victoria Cross)? 1066 浏览
- 什么是胭脂论坛(Rouge Forum)? 923 浏览
- 什么是Thinko(Thinko)? 1184 浏览
- 什么是婴儿学步车(Baby Walker)? 945 浏览
- 布尿布的优点是什么(Advantages of Cloth Diapers)? 841 浏览
- 什么是雪人(Snowman)? 927 浏览
- 我怎么能不感到内疚地说不呢(Say No Without Feeling Guilty)? 613 浏览
相关问题
0 条评论
请先 登录 后评论
admin
0 篇文章
作家榜 »
-
 xiaonan123
189 文章
xiaonan123
189 文章
-
 汤依妹儿
97 文章
汤依妹儿
97 文章
-
 luogf229
46 文章
luogf229
46 文章
-
 jy02406749
45 文章
jy02406749
45 文章
-
 小凡
34 文章
小凡
34 文章
-
 Daisy萌
32 文章
Daisy萌
32 文章
-
 我的QQ3117863681
24 文章
我的QQ3117863681
24 文章
-
 华志健
23 文章
华志健
23 文章
推荐文章
- 什么是活动宴会(Movable Feast)?
- 我的东西太多了吗(Too Much Stuff)?
- 什么是琥珀出牙项链(Amber Teething Necklace)?
- 什么是心灵遥控(Telekinesis)?
- 什么时候寄宗教贺卡合适(When is It Appropriate to Send Religious Greeting Cards)?
- 什么是钟表学家(Horologist)?
- 什么是可恶的雪人(the Abominable Snowman)?
- 瓶子里的信息是什么(Message in a Bottle)?
- 什么是詹森主义(Jansenism)?
- 什么是PSAT考试(PSAT Exam)?
- 什么是暴利(Windfall)?
- 我的孩子需要家教吗(my Child Need a Tutor)?
- 什么是干狗粮(Dry Dog Food)?
- 什么是谋杀性(Murderabilia)?
- 什么是雪撬(Snow Sled)?
- 什么是曼尼(Manny)?
- 什么是抗病毒组织(Antiviral Tissue)?
- 什么是救援刀(Rescue Knife)?
- 什么是印模(Moulage)?
- 什么是Caboodles&Reg;(Caboodles&Reg;)?
- 什么是预感(Hunch)?
- 阿舒拉节是什么日子(Day of Ashurah)?
- 什么是借来的(Lent)?
- 什么是表演(Showmance)?
- 如何简化部首(Simplify Radicals)?
- 什么是化学药品(Chemical Cosh)?
- 什么是手榴弹(Hand Grenade)?
- 什么是不明飞行物热点(UFO Hotspots)?
- 什么是闲聊(Chitchat)?
- 什么是活页本(Loose Leaf Notebooks)?