从水龙头下落的水为何会越来越细？

图片：kaboompics / CC0

姜小白71，力学

这个问题是射流现象(Fluid Jet or Jet)中最简单的一个问题，一般称为Free-Falling Fluid Jet问题。即便如斯，因为流体力学的复杂性，至今仍有学者在孜孜不倦地研究着这个问题。

当然，若是只是为领会释糊口中的常见环境，那么现有研究成果仍是足够的。我们起首心猿意马性地看一下这个问题，从水龙头中流出的水在重力的感化下不竭加快，是以流速是越来越大。而又因为流量守恒，截面积只会越来越小（流量=截面积 x 流速），是以水柱越来越细。接下来我们来心猿意马量计较一下，这时辰就需要相关的流体力学常识了。

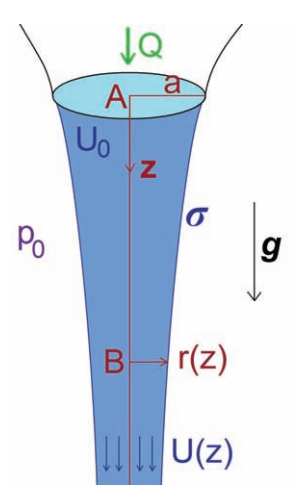
如上图所示，我们考虑的流动是大雷诺数流动，此时流动可视为无粘流动(现实上水的粘性自己就很小)，但同时需要包管流动仍是层流。那么此刻流动可看作简单的一维流动，我们可以在

$A,B$

两点之间利用伯努利方程。

$\frac{1}{2}\rho U_0^2+\rho g z+P_A=\frac{1}{2}\rho U^2(z)+P_B$

考虑流量守恒则有

$Q=2\pi\int_0^r U(z)r(z)dr=\pi a^2U_0=\pi a^2U(z)$

考虑下面两种环境，

（1）忽略概况张力。

此时

$P_A=P_B=P_0$

,按照上面两式，可解得，

$\frac{r}{a}=\left(1+\frac{2gz}{U_0^2}\right)^{-1/4}$

$\frac{U(z)}{U_0}=\left(1+\frac{2gz}{U_0^2}\right)^{1/2}$

这就是水流半径和流速随高度的转变关系式。当然，我们完全可以将水流理解为自由落体活动的，只是为了形式的同一性，才用伯努利方程暗示。下面跟尝试成果对比一下。

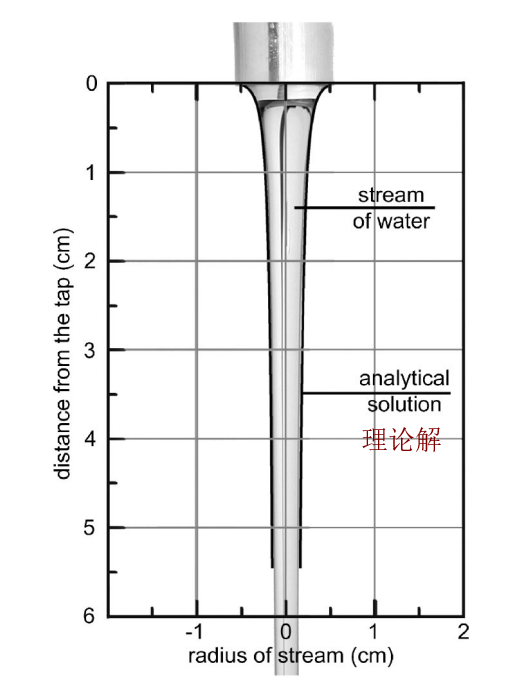
可以看到，上述理论成果与尝试成果合适杰出。若是要诠释糊口的现象，上面的公式就足够了。为了知足大师的进修热情，下面我们起头进一步的阐发，这就是第二种环境。

（2）考虑概况张力。

按照 Young-Laplace 公式（不领会的话可拜见我的其他回覆），

$P_A\approx P_0+\frac{\sigma}{a}$

$P_B\approx P_0+\frac{\sigma}{r}$

按照伯努利方程和流量守恒，解得

$\frac{r(z)}{a}=\left(\frac{U0}{U(z)}\right)^{1/2}=\left[ 1+\frac{2}{Fr}\frac{z}{a}+\frac{2}{We}\left(1-\frac{a}{r} \right)\right]^{-1/4}$

式中，

$Fr=\frac{U_0^2}{ga}$

称为 Fr 数（Froude Number）,表征惯性力和重力的相对巨细。

$We=\frac{\rho U_0^2a}{\sigma}$

称为 We 数（Weber Number）,表征惯性力和概况张力的相对巨细。

这个公式插手了概况张力批改，是以合用规模更广。而在日常糊口中的水龙头流水现象中，We 数一般比力大，是以公式中的最后一项可以忽略失落，又回到了第一种环境，这意味着我们忽略概况张力是合理的。但要明白的是，我们是在无粘前提下进行会商的，若是考虑粘性的话，环境就更复杂了，良多文献提出了各类粘性耗散的估量方式，有感乐趣的读者可进一步参阅文末参考文献。我注重到有良多人提到如下图所示的水柱被拉断并形当作液滴的环境，这其实是因为Plateau-Rayleigh 不不变性(The Plateau-Rayleigh Instability)，有机遇再答吧。

【参考文献】

【1】Massalha, T., & Digilov, R. M. (2013). The shape function of a free-falling laminar jet: Making use of Bernoulli's equation.American Journal of Physics,81(10), 733-737.

【2】Grubelnik, V., & Marhl, M. (2005). Drop formation in a falling stream of liquid.American journal of physics,73(5), 415-419.

【3】Gamez-Montero, P. J., Castilla, R., Freire, J., Khamashta, M., & Codina, E. (2016). An empirical methodology for prediction of shape and flow rate of a free-falling non-submerged liquid and casting iron stream.Advances in Mechanical Engineering,8(9), 1687814016669635.

发表于 2019-04-11 22:55
阅读 ( 1282 )
分类：其他类型

从水龙头下落的水为何会越来越细？

你可能感兴趣的文章

相关问题

0 条评论

作家榜 »

推荐文章