优博地址

 知乎用户,以诚为本,以朴修身,以勇求进,以毅立功
知乎用户,以诚为本,以朴修身,以勇求进,以毅立功
进修数学范畴的一门科目标根本常识,无外乎两个目标,一个是在测验中取得好成就,一个是在理解这些常识中,能在本身的研究顶用到它。前一个目标良多回覆已经归纳综合的很好,这里不再赘述,所以呢,就连系本身从上课到学做研究的一些体味来办事于第二个目标读者。
一门学科入门,有两种方式,一种是从抽象到具体,一种是从具体到抽象。一起头就是一个很严密的抽象的界说,以及随之而来的一系列公式,对新手其实并不是很友爱,并且也并不克不及帮忙初学者细心的思虑这些公式和界说所蕴含的人类聪明。所以,我们就先从一些具体的案例出发,看看为啥线性代数里有那么多如“线性相关”似乎很无聊的概念以及环绕这些概念而来的理论吧。我们考虑三个比力根本的案例:线性方程组的求解;线段扭转与线性变换;以及高维数据降维与聚类。前两个是很经典的问题,最后一个是跟着统计学出格是大数据时代到来变得在分歧学科遍及呈现的问题。让我们起头吧。
1.案例 1:线性方程组的求解
从小学起头,我们就起头进修若何求解下面的方程组(这个方程组里,
是未知数,其他为已知数,m 纷歧心猿意马等于 n):
方程组(1)简练而又主要,因为很多理论以及简单的模子最后都可以归结为方程组(1)的求解。小学和初中进修的是加减消元法,高中后,算立体几何题,求法标的目的量的时辰,会用到行列式来求解这个方程组。上大学前,我们对于线性代数最根基的问题,线性方程组的求解,并不是很目生。
不外,在读者眉飞色舞的吭哧吭哧的求解方程组(1)的时辰,或许想过,以及在具体的算例中碰着过如下问题:
- 方程组(1)与方程
- 若何对行列式做到 n 个变量的推广呢?与此相伴的问题时,行列式的事实该若何界说呢?
- 方程组(1)什么时辰有解,什么时辰没有解,什么时辰诠释独一的,什么时辰解是不惟一的呢?
这三个问题,恰是一本尺度的线性代数教材里的前几章的常识所致力于回覆的问题。解决思绪就是引入标的目的量空间,以及矩阵,那么(1)式可以形式上的写作:
我们只要研究系数矩阵
以及增广矩阵
就好了。怎么研究呢,那些絮絮不休的线性相关的理论就是为此办事的。
若是我们考虑我们熟悉的实数域的环境,当系数矩阵是方阵时,我们将行列式视作空间
到数域
的映射,即:
若是我们按照一阶行列式,二阶行列式的公式,递归的界说行列式
可以证实(3)是独一知足如下前提的映射:
1)将单元矩阵
映射为 1
2)
此中省略号的行标的目的量都是一样的;
3) 若是矩阵
相邻的行标的目的量不异,那么
用行列式,线性相关,基,秩这些概念,我们便可以成立起关于方程
的有解的判别前提,以及解的布局的心猿意马理 ,这些尺度的教材里都有,就不再赘述了。值得注重的是,若是我们将这套理论,移植到可微函数构成的线性微分方程组,我们也可以机关近似的命题,这申明我们可以将 矩阵和标的目的量做更为一般的推广。
2. 案例 2,线段扭转与线性变换
若是读者用过 PS 或者 PPT 的时辰,会发现里面的那些外形其实都是用坐标描述的,于是我们便可以将其视作
的一个子空间。考虑一个简单的问题,我们需要对 PS 里位于坐标原点的一段线段逆时针扭转必然的角度,PS 是若何实现这个功能的呢?很简单,我们只需要对这段线段对应的标的目的量进行坐标变换就好了。若是进行变换呢?若是我们将方程(2)视作将标的目的量 x 变换为标的目的量 b,那么我们可以把矩阵 A“视作”一个变换。那么我们只要用一个二阶矩阵来暗示扭转变换就好了,这个二阶矩阵,可所以
扭转变换是更为称为线性变换的具体案例,并且不改变线段的长度(连结距离)。此外,我们可以想象,若是一个标的目的量的偏向与扭转的偏向一致,那么扭转变换是不会改变其偏向的(这个标的目的量就是所谓特征标的目的量)。
尺度的线性代数教材的后半部门,很大水平上是对这个线段扭转问题的扩展。矩阵的特征值,对角化,以及二次型的理论就是上面这个线段扭转问题的进一步研究。此外,二次型的相关理论还可以帮忙我们回覆二次曲线和曲面分类的问题。具体可见任何一本尺度的线性代数教材,例如丘维声的书,这里不再赘述。
3. 案例 3:高维数据降维与聚类
这个案例和笔者的专业很是相关了。素质上来说是数理统计与线性代数的交叉。
当前生物研究中有一个很是前沿的手艺,叫做单细胞转录组测序。例如我们可以从人身上抽外周血,进行单细胞测序,这些测序数据在颠末一系列的处置之后,最终会获得一个称之为表达矩阵的对象,此中每一行对应一个基因,每一列对应一个细胞,所以这个数据真的是一个矩阵。若是读者看过《工作细胞》的话,或许知道外周血里有很多分歧类型的细胞,好比 T 细胞,B 细胞,这些细胞之所所以分歧的,真的是因为他们形态和功能特异。那么我们会问,可否从这么多细胞的表达谱将分歧的细胞类型找出来呢。当然是可以的。
假如我们测了 2700 个单细胞,人的参考基因组注释出了 30000 个基因的话,那么我们的表达矩阵应该是
的十分稀少的矩阵。我们但愿能在二维的坐标图中,尽可能的展示出细胞类型的信息,而且能区分出分歧的细胞类型。转化为两个子问题,那就是,高维矩阵降维,以及高维数据聚类的问题 。这中心有很多巧妙的算法。在实践中,高维矩阵降维我们常用的是 PCA,t-SNE,UMAP 等算法,而聚类的话,我们会用条理聚类以及 Louvain Algorithm 之类的图聚类算法,对每个细胞对应的高维标的目的量进行聚类;
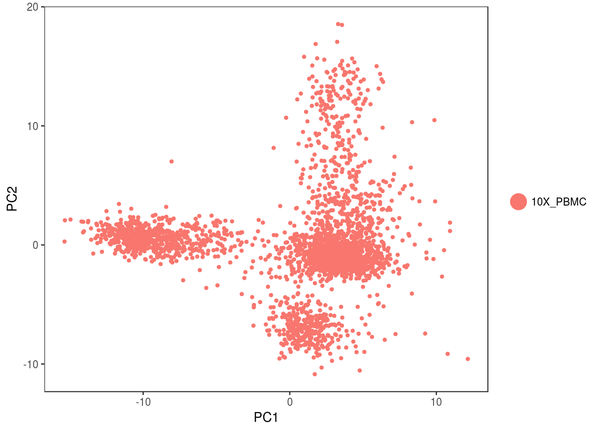
我们可以看看具体的步调,这是 PCA 的成果,我们看到,细胞似乎能分为 4 个分歧的大类 ;
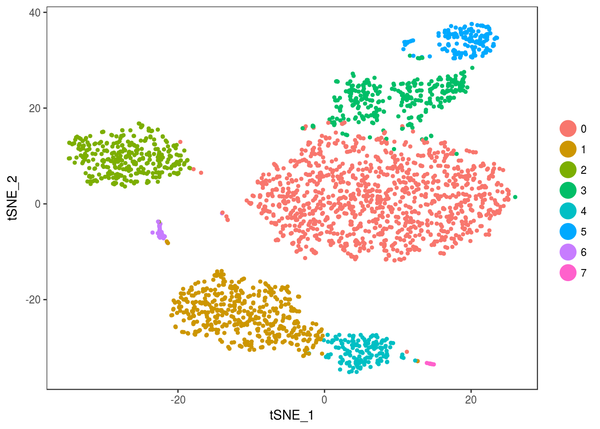
我们用非线性的降维方式 t-SNE,将这些细胞在二维的投影上分的更开,而且用 Louvain Algorithm,进行聚类 ,将聚类标签,用分歧颜色展示出来;
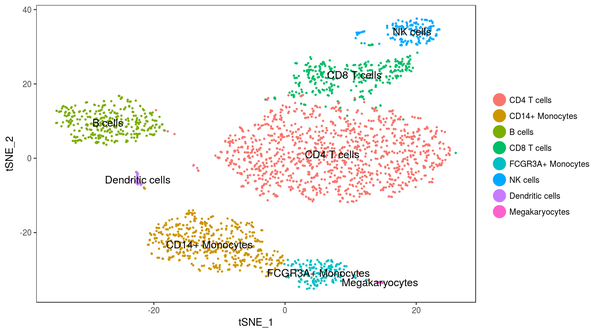
若是连系先验常识,查看每个类别对应细胞的差别表达基因,我们可以对每个类别进行注释,最终我们可以获得下面的这个成果:
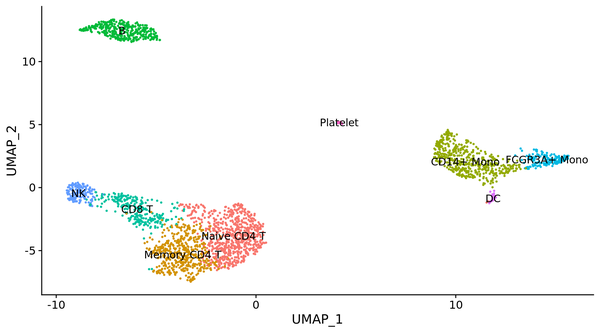
此外 ,还可以将 PCA 以及 t-SNE 纳入到流形进修的框架里,有学者提出了 UMAP 算法 ,可以或许更好的可视化,降维与聚类成果。
PCA,t-SNE,以及 UMAP 这些统计进修里的高级算法背后离不开矩阵阐发和泛函阐发(可以将其视为函数版本的线性代数)的相关理论,其策略就是界说怀抱空间以及范数,这里就不再做深切介绍了。只列出参考文献:
PCA 的介绍可见李航的《统计进修方式》;
t-SNE 道理以及代码实现见
UMAP 论文以及代码实现见
- 发表于 2019-10-20 17:30
- 阅读 ( 1784 )
- 分类:其他类型
你可能感兴趣的文章
- 2019武汉军运会怎么购买门票 890 浏览
- 如果把U盘插在充电器上会怎么样 2348 浏览
- 不能初始化Photoshop,暂存盘已满怎么办 1114 浏览
- 淘宝开店店铺简介怎么写 953 浏览
- 加泰罗尼亚为什么闹独立? 1064 浏览
- 一个社会主义者对苏联灭亡根源的解读是什么? 979 浏览
- 人类是否真的是被困在地球上的囚徒?结果颠覆认知 958 浏览
- 高数学天赋的孩子应该获得怎样的教育? 1230 浏览
- 为什么司法使命在于“创新”或者“诠释”? 1040 浏览
- 都盯上了月球南极,那么南极到底发现了什么? 948 浏览
- 双黄蛋会孵出什么样的小鸡? 1144 浏览
- 用数学来理解:人数的优势究竟在战争中占据什么样的地位? 992 浏览
- 骰宝游戏 878 浏览
- 经期心情烦躁怎么办,6招缓解经期情绪急躁症 1101 浏览
- 宝宝吃益生菌有哪些好处 761 浏览
- 如何选择墨镜 880 浏览
- 明仕 857 浏览
- 博猫彩票 901 浏览
- QQ空间农场中如何领取系统停机维护礼物 920 浏览
- 如何给图片添加彩色铅笔效果 958 浏览
- 上海一女漫画家出租屋内意外离世,漫画家的压力究竟有多大? 894 浏览
- 瞎扯 · 如何正确地吐槽 898 浏览
- 汽车车身是越硬越安全吗? 1513 浏览
- 利博 870 浏览
- 精子是怎么在茫茫子宫中找到小小卵子的? 1490 浏览
- 怎么管理能力比你强的下属? 1392 浏览
- 网络老虎机 1081 浏览
- 辞职报告范文怎么写 789 浏览
- 小个子打篮球技巧 860 浏览
- 打好篮球要掌握哪些技巧 785 浏览
相关问题
0 条评论
0 篇文章
作家榜 »
-
 xiaonan123
189 文章
xiaonan123
189 文章
-
 汤依妹儿
97 文章
汤依妹儿
97 文章
-
 luogf229
46 文章
luogf229
46 文章
-
 jy02406749
45 文章
jy02406749
45 文章
-
 小凡
34 文章
小凡
34 文章
-
 Daisy萌
32 文章
Daisy萌
32 文章
-
 我的QQ3117863681
24 文章
我的QQ3117863681
24 文章
-
 华志健
23 文章
华志健
23 文章
推荐文章
- 玫瑰花花苞还没开就焦枯了是怎么回事
- 日本雅虎邮箱如何修改密码
- matlab find用法
- Vue如何新建项目及Vue
- 视频怎么换封面
- 七天娱乐
- 表格怎样设置点到某单元格时所在行颜色有变化
- 水果竞猜
- 怎么查询对方qq的ip地址 如何通过qq查看对方ip
- win10和win7双系统如何跳过开机自检磁盘
- 企业邮箱怎么绑定qq邮箱
- 启动CAD提示文件加载安全问题怎样解决
- 怎么样在公众号植入直播
- 如何提高月季扦插生根后假植成活率
- 淘宝卖家怎么找货源
- 盆栽朱顶红什么时候换盆合适
- SQLyog如何创建触发器,详细教程
- SQLyog如何备份数据库,详细教程
- 山西娘子关游玩攻略
- 北京园博园一日游攻略
- 驾车遇险应该怎么急救
- 新不夜城论坛
- 可爱女宝形象设计
- 名人宣传画设计
- 拔河规则及技巧
- 如何使用健腹轮
- 口袋妖怪最强进化3.0普通版攻略
- 王者荣耀周瑜战令限定皮肤赤莲之焰怎么获得
- 王者模拟战精灵阿鸡怎么获得
- 王者荣耀兰陵王战令限定皮肤训魔猎人怎么获得