【MATLAB】多项式的四则运算和微积分运算

多项式之间可以进行四则运算，结果仍然为多项式。在MATLAB中，通过系数向量进行计算，结果仍为系数向量。本经验中所用MATLAB软件版本为R2020a。

东西/原料

1
多项式的加减运算。没有相关的函数，现实上加减运算就是系数标的目的量的加减运算，只要将系数对其即可。
2
多项式的乘法运算。利用conv函数实现，挪用格局为：
p=conv(p1,p2)
3
多项式的除法运算。利用deconv函数实现，挪用格局为：
[q,r]=deconv(p1,p2)，此中q为商式，r为余式。
4
多项式的微分。利用polyder函数，挪用格局为：
p=polyder(p1)，求多项式p1的导数；
p=polyder(p1,p2)，求多项式p1*p2的积的导数；
[p,q]=polyder(p1,p2)，p1/p2的导数，p为导数的分子多项式系数，p为导数的分母多项式系数。
5
多项式的积分。利用polyint函数，挪用格局为：
I=polyint(p,k)，求以p为系数的多项式的积分，k为积分常数项；
I=polyint(p)，求以p为系数的多项式的积分，积分常数默认为0。
6
多项式部门分式睁开。利用residue函数，挪用格局为：
[r,p,k]=residue(B,A)，B为分子多项式系数标的目的量，A为分母多项式系数标的目的量，k为余式多项式行标的目的量。p为顶点列标的目的量，r为零点列标的目的量。
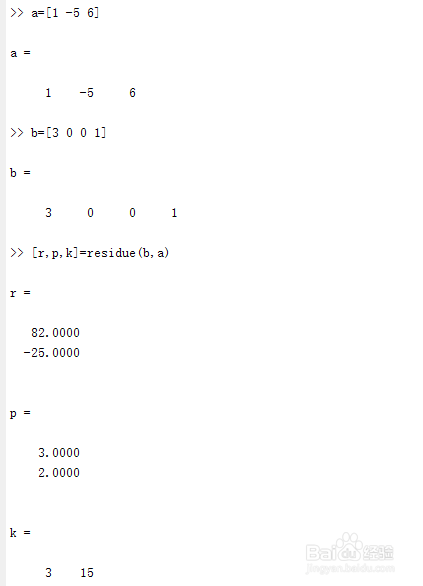END