有哪些有趣的概率问题？

图片：TymonOziemblewski / CCO

张翼腾，复旦大学数学系

风险投资陷阱：做的每一笔投资都是正收益的，可是最后几乎会变得一无所有。

在进行投资或者采办股票的时辰，预期收益是一个很是主要的参考。当今越来越多的人接管概率的不雅点，知道固然买彩票或者赌钱有可能暴富，可是因为从期望角度而言每买一张彩票或者是下一个赌注都是吃亏的，所以从理性角度不该该进行这一笔买卖。

可是收益为正的投资必然是理性的么？

我们设想有这样一种风险投资：若是当前的的资产为 S 的话，下一个单元时候的资产 50%的概率变为本来的 0.9 倍，50%的概率酿成本来的 1.11 倍。问题是：持续进行这样的投资是否是理性的。

颠末简单的计较可以获得，颠末一个单元时候后，资产的数学期望是

$(0.9\times 0.5 + 1.11 \times 0.5) S= 1.005S$

，这样预期收益为

$0.005S$

，也就是说，该投资单元时候的期望收益率为 0.5%。

也许看到这里你会感觉，不竭进行这样的投资是无比理性的，看起来每一笔投资都无比的乐不雅。可是事实上，若是一小我不竭进行这样的投资，他几乎会满盘皆输。

我们用数学说话来描述这个问题：若是最初的资产是

$S_0$

，

$n$

个单元时候后的资产

$S_n$

是

$S_{n-1}$

的

$1+\eta_n$

倍，

$\eta_1,\eta_2,\dots$

之间是自力的，有 50%的概率为 0.11，50%的概率为 -0.1。那么

$S_n = S_0(1+\eta_1)(1+\eta_2)\dots(1+\eta_n)$

。

因为自力性，

$\mathbb{E}(S_n) = S_0\mathbb{E}(1+\eta_1)\mathbb{E}(1+\eta_2)\dots\mathbb{E}(1+\eta_n) = 1.005^nS_0$

。是以

$\lim_{n\rightarrow\infty}\mathbb{E}(S_n) = +\infty$

，也就是说理论上投资期望收益是正无限。

可是

$S_n = e^{\ln S_0 + \ln(1+\eta_1) + \ln(1+\eta_2) + \dots+\ln(1+\eta_n)}$

，

$\ln(1+\eta_n)$

有 50%的概率为

$\ln 0.9$

，50%的概率为

$\ln 1.11$

，所以

$\mathbb{E}[\ln (1+\eta_n)] = \ln 0.999 < 0$

。按照壮大数心猿意马律，

$\mathbb{P}(\sum_{n=1}^\infty \ln(1+\eta_n) = -\infty) = 1$

，也就是说

$\mathbb{P}(\lim_{n\rightarrow \infty}S_n = 0) = 1$

，即几乎可以必定不竭进行这样的投资会血本无归。

到这里读者可能会发生猜疑，明明期望是正无限为何几乎血本无归呢？这是因为尽管

$S_n$

趋于零，可是

$\mathbb{E}S_n$

趋于正无限，就是说可能存在

$S_n$

很大很大，当然这种工作发生的概率很是很是小。成果导致很少的人赚良多的钱，可是绝大部门人血本无归。

为了验证这一不雅点，我利用蒙特卡洛方式进行了数值上的模拟。我一共模拟了一万个投资者，初始资产都为 1，履历了 300 个单元时候。模拟的成果如下：

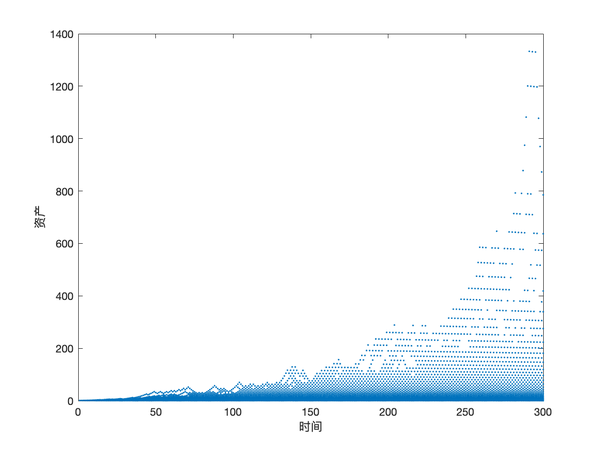
每一点代表了对应时候一个投资者的资产。我们可以看到，跟着时候的推进，越来越多的投资者的资产越来越少，可是与此同时，少少数投资者获得了惊人的利润。也就是说，固然社会总资产看起来是不竭增添的，可是背后埋没的是社会上绝大部门的资产会把握在少少数人的手里，和绝大部门人会血本无归。

这就是风险投资中的陷阱：看上去无比乐不雅的投资却屡屡吃亏，明明理论上投资的期望收益是正无限，可是市场上几乎没有真正赚钱的投资者。

所以在赌场中，即使是一个赌神，可以或许做到每次赌钱的期望收益都是正的（这几乎不成能实现），若是他赌性很大（每次都压良多的钱，根基全压）的话，到头来也根基上血本无归，真正可以或许经由过程赌钱赚钱的人是及其罕见的。

凯利公式

评论区 @Zhang Wang 提到了凯利公式，我也挺感乐趣，下面我就来继续会商每次投资的时辰应该投资当前总资产的最优比例（仓位）

$F^*$

。

下面我们对遍及环境进行会商，收益率

$\eta$

从命某种分布而且知足

$\eta\geq -1$

，那么若是我们每次投资选择的仓位为

$F$

的话，现实收益率变为

$F\eta$

，按照之前的会商我们知道，

$S_n^{1/n} = e^{\frac{\ln S_0 + \ln(1+F\eta_1) + \ln(1+F\eta_2) + \dots+\ln(1+F\eta_n)}{n}}$

，按照壮大数心猿意马律

$S_n^{1/n}\mathop{\rightarrow}^{a.s.}e^{\mathbb{E}[\ln(1+F\eta)]}$

，也就是说平均收益率几乎可以必定收敛于

$e^{\mathbb{E}[\ln(1+F\eta)]}$

，所以最优投资方案应该知足

$F^* = \mathop{\arg\max}\limits_{F\in [0, 1]}(\mathbb{E}[\ln (1+F\eta)])$

，令

$\phi(F) = \mathbb{E}[\ln(1+F\eta)]$

，

$\phi'(F) = \mathbb{E}[\eta/(1+F\eta)]$

，

$\phi''(F) = \mathbb{E}[-\eta^2/(1+F\eta)^2]<0$

。

若是

$\mathbb{E}[\eta]\leq 0$

的话，

$\phi'(F)\leq \phi'(0)\leq 0$

，

$\phi(F)$

关于

$F$

单调下降，所以

$F^* = 0$

，也就是说，在期望为负的投资中，最优选择是一分钱都不投资。

若是

$\mathbb{E}[\eta] > 0$

的话，

$\phi'(0) = \mathbb{E}[\eta] > 0$

，因为

$\phi(F)$

是上凸函数，若是

$\phi'(1) = \mathbb{E}[\frac{\eta}{1+\eta}]\geq 0$

，申明

$F^* = 1$

，申明此时的最优选择是仓位拉满。

若是

$\phi'(1) = \mathbb{E}[\frac\eta{1+\eta}]<0$

，那么最优选择知足

$\phi'(F^*) = \mathbb{E}[\frac\eta{1+F^*\eta}] = 0$

。

若是进行线性近似的话，

$0 = \mathbb{E}[\frac\eta{1+F^*\eta}] \approx \mathbb{E}[\eta - F^*\eta^2]$

，也即

$F^*\approx \frac{\mathbb{E}[\eta]}{\mathbb{E}[\eta^2]}$

。

对于最简单的环境，

$\eta$

从命两点分布，

$\mathbb{P}(\eta = t^+) = p$

暗示以概率 p 收益率为

$t^+$

，

$\mathbb{P}(\eta = -t^-) = q$

暗示以概率

$q = 1-p$

收益率为

$-t^-$

，此中

$t^+>0, -t^-<0$

别离暗示挣钱和吃亏的环境。

那么按照之前的阐发，投资有意义的充要前提为

$pt^+ >qt^-$

，在这种环境下，若是

$p \frac{t^+}{1+t^+} > q\frac{t^-}{1-t^-}$

，此时仓位拉满。

不然，最优仓位知足

$p\frac{t^+}{1+F^*t^+} = q\frac{t^-}{1-F^* t^-}$

，化简获得

$F^* = \frac{p}{t^-} - \frac q{t^+} = \frac{pt^+ - qt^-}{t^+t^-}$

。这就是投资中的凯利公式。

当然可以直接计较

$F^* = \frac{p}{t^-} - \frac q{t^+} = \frac{pt^+ - qt^-}{t^+t^-}$

，若是

$F^*\leq 0$

，那么遏制投资；若是

$F^*\geq1$

，那么投资拉满；若是

$0<F^*<1$

，那么每次投资总资产的

$F^*$

。

那么对于上文中提到的具体投资问题，

$F^* = \frac{5}{11}$

。

在这个问题下 @横砚等 268 人提到了这个问题：

假设有一个游戏，人物的进犯力为 0～10，怪物的生命值为 10，不考虑防御、闪避、射中率等身分，那我平均进犯几回可以杀死一个怪物？

@cyb 酱给出了用递推解决了这个问题。我用直接计较的体例来计较这个概率。

我们把这个问题数学化，

$X_1, X_2, \dots, X_n, \dots$

是自力同分布随机事务，代表人物每一次进犯造当作的危险，怪物的血量是 M ，那么需要进犯的次数

$T = \min\{t| X_1+\dots +X_{t}\geq M\}$

。求问：

$\mathbb{E}(T)$

。

因为

$T$

取值为正整数，所以

$\mathbb{E}(T) = \sum_{k=1}^{\infty}\mathbb{P}(T\geq k)$

。在这道题中，

$\mathbb{E}(T) = \sum_{k=1}^{\infty}\mathbb{P}(T\geq k) = \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k-1} < M)$

。

分为两种环境：

第一种环境是人进犯造当作的危险是持续的，也就是说是

$[0, M]$

之间的平均分布（

$X_i\mathop{\sim}^{i.i.d.} U([0, M])$

）。

另一种环境是人进犯造当作的危险是离散的，也就是说是

$\{0, 1,\dots , M\}$

上的平均分布。

第一种环境计较

$\mathbb{P}(X_1+\dots+X_{k-1}< M)$

显然是一个几何概型，对于

$k>1$

时，总样区域对应着

$k-1$

维的边长为 M 的立方体，而使得不等式当作立的区域是一个

$k-1$

维的锥体（二维时对应着直角三角形，三维时对应着三棱锥），体积为

$\frac{1}{(k-1)!}M^{k-1}$

，是以

$\mathbb{P}(X_1+\dots+X_{k-1}< M) = \frac{1}{(k-1)!}$

。

$\mathbb{E}(T)= \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k} < M) = \sum_{k=1}^{\infty} \frac1{(k-1)!} = e$

。

第二种环境稍微复杂一点，计较

$\mathbb{P}(X_1+\dots+X_{k-1} < M)$

对应着一个古典概型，总事务数显然是

$(M+1)^{k-1}$

。我们可以把

$X_1+\dots+X_{k-1} < M$

对应的事务拆分当作

$M$

个子互斥事务：

$X_1+\dots+X_{k-1} = s, s=0,1,\dots, M-1$

。

按照组合常识，

$X_1+\dots+X_{k-1} = s$

对应的事务数量为：

$\binom{s+k-2}{k-2}$

。所以

$\mathbb{P}(X_1+\dots+X_{k-1} < M) = \frac{\sum_{s=0}^{M-1}\binom{s+k-2}{k-2}}{(M+1)^{k-1}}= \frac{\binom{M+k-2}{k-1}}{(M+1)^{k-1}}$

。

$\mathbb{E}(T)= \sum_{k=1}^{\infty}\mathbb{P}(X_1+\dots+X_{k} < M) = 1+\sum_{k=2}^{\infty} \frac{\binom{M+k-2}{k-1}}{(M+1)^{k-1}} = (1+\frac1M)^M$

。对应

$M=10$

的成果为：2.59374246。

发表于 2019-08-06 23:33
阅读 ( 1501 )
分类：其他类型

有哪些有趣的概率问题？

你可能感兴趣的文章

相关问题

0 条评论

作家榜 »

推荐文章