可以无偿获得 5000 元，但有 1/100 万的几率当场毙命，你会玩多少次这样的游戏？

图片：《动物宿世界》

标的目的日葵人生，伴侣来了有好酒，虎豹来了有猎枪

这个问题很有意思，花 10 分钟看完这个回覆，你可能会从底子上改变你对这个问题的判定

和对人生的理解

以及趁便学点金融常识

一，玩几多次我会妥妥地挂失落？

这其实是一个简单的概率学问题

百万分之一的发生概率，也就是不发生的概率是 99.9999%

我们先科普一下，假设 A 事务发生的概率是 40%（那对应不发生的概率就是 60%），B 事务发生的概率是 40%，那么 A 事务和 B 事务都发生的概率是几多呢（假设两者是自力事务，两者互不影响）？

谜底是：40%*40%=16%

所以对于一系列自力事务而言，他们都发生的概率就是他们发生的概率的乘积

或者，同样的，他们都不发生的概率就是他们各自不发生概率相乘的积。

那么，回到这个问题，为了便利我们决议计划，我们可以先计较出持续测验考试若干次（一千次、一万次）而不挂失落的概率是几多，我相信环境会加倍明白。

假设，我们玩 1000 次，可以或许获利 5000*1000=5000000，也就是 500 万元

那么玩 1000 次都不出事儿的概率是几多呢？99.9999%的 1000 次方，简单用计较器算一下，就可以得出下面这张作死的收益与对应出事儿概率的统计表。

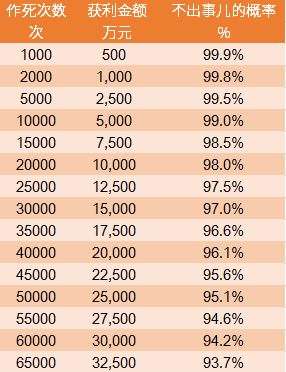
可以看到，当我们玩这个游戏 1000 次时，我们能赚 500 万元，有 99.9%的概率我们还在世

因为翻车的这个概率其实太低了，百万分之一

所以即使我们往后推算良多次，存活概率依然不小

好比我们为了赚 2.5 亿测验考试了 5 万次时，我们有 95%的概率还在世

99%和 95%其实没有本色性不同，但收益从 500 万跳涨到了 2.5 亿

那当我们测验考试几多次之后，我们的生还概率会低于 10%呢？

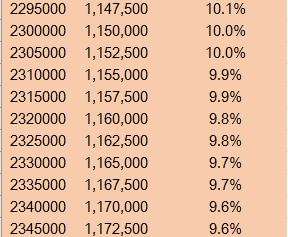
也就是，我们若是持续测验考试 231 万次，次次生还，依然健在的概率只有 10%（原文有歧义，已更改），但这个时辰，我们已经赚了 115.25 亿人平易近币，半斤八两于马云 2018 年净资产的……6%

马云爸爸的钱是真的多啊

到底要什么时辰激流勇退，回头是岸？

当然，概率和发生是两回事，这也就是我们金融上所说的风险

风险不是指会发生的坏工作，而是指坏工作发生的概率

正常环境下，我们所做的所有工作，都是有收益的，否则我们不会去做

正所谓全国熙熙，皆为利来；全国攘攘，皆为利往

但享受收益的同时，也会有风险

人有多斗胆，地有多大产就是这个意思

就像我们买国债，会有利钱，这是我们的收益；但我们也有本金损掉的风险（我国政权衰亡、当局破产），但我国作为一个负责任的大国，这种环境发生的概率微乎其微，可以忽略，所以我们可以视国债的收益为无风险收益

但无风险的环境是少少且特别的，并且因为没有风险，所以收益很低

正常环境下，收益越高，风险越大，相信看了上面那张表后，大师会有很直不雅的感触感染

大师在日常糊口中，只要赚取收益，工作也好、存钱也好、买理财也好、买股票衍生品也好

都是为了赚取收益，但同时也会权衡风险，只是大师没有这么专业的常识，不会算的很清晰

但大师都大白，股市有风险，入市需谨严。

朴实的风险节制意识，大师都有，只是强弱有别。

那收益多高算收益高呢？多大风险算风险大呢？

分歧的人有分歧的谜底，这个在金融学中有个专业的形容词，叫风险偏好

为了便于理解，我们先忽略讲义的概念，简化一下对风险偏好的描述。给大师一个直不雅印象

有人厌恶冒险，本能的会规避有风险的投资选择——好比直接不玩这个游戏，这种叫风险厌恶型投资者

有人感觉风险和收益匹配的前提下，为了更高的收益冒点风险也值得——好比 @孙瑞昊的回覆，感觉玩 1000 次，能赚 500 万，99.9%的概率还在世，那就值得测验考试，这是大大都人的状况。这叫风险中性型投资者。

当然，有厌恶就有爱好，宿世界上就有这么一群人，秉持富贵险中求的人生哲学，风险越高，越刺激，越爽，好比——赌徒。对于他们而言，若是收益足够高，哪怕只有 10%的胜率，也会去博一次。这就是风险爱好型投资者。

所以什么时辰激流勇退，金盆洗手，分歧的人有分歧的谜底。

三、为什么这个问题下，风险厌恶者这么多？

正如题本家儿总结的，本来预估至少 90%的人会玩这个游戏

但现实上 30 个回覆里有接近一半的人选择了不玩这个游戏

这较着不合适我们所说的，风险中性才是大大都人的常态的比例

为什么呢？

因为对于分歧后果，大师会形当作分歧的风险偏好。

好比，若是这个问题的设置是，若是百万分之一的概率会损掉所有所得，或者会损掉 1 块钱

那么可以预期，大师城市选择玩到本身手断为止

但这个标题问题的不良后果设置是掉去生命，对大大都人而言，在掉去生命这个成果上，大部门人都是风险厌恶者。只要听到有生命危险，大师城市本能的退避三舍

所以，这个比例低于提问者预期，并不奇异

因为大师都不肯意拿本身生命恶作剧，哪怕概率很低很低。

四、那要怎么晋升大师介入的意愿呢？换个问法就可以

就像前面所说的，风险意识大师都有，可是绝大大都非金融经济相关专业的人

风险意识都很朴实，对于要承担多大的风险只有很恍惚的概念

大师不仅对风险没有太具体的概念，对太高的收益也没有太具体的概念

#贫穷限制了我的想象系列#

一说到“你的生命会有危险”，大师会本能的规避，才会有 40%多的答本家儿选择敬而远之

但这本家儿如果因为大大都人对于“百万分之一”这个概率，没有直不雅的熟悉

其实，百万分之一的概率，长短常很是很是很是低了。

若是我们把我们日常的工作列一个概率，我们会发现，我们天天都在冒着各类生命危险

大大都都不比百万分之一高

我们换个问法，若是给你 5000 块，让你坐一次飞机，你愿意吗？

或者给你 2500 万，让你打的 200 次，你愿意吗？

我相信没有几小我会说不肯意，究竟结果，飞机是现今朝最平安的交通东西

那飞机发生空难的概率是多大呢？比来 5 年，每百万个航班发闹事故的 5 年均值为 0.58 次，也就是坐飞机不出事儿的概率是 99.999942%——很是接近我们所说的，玩 1 次出事儿的概率 99.9999%

碰到空难的概率有多大

也就是说，你玩 5000 次都不出事儿的概率，和坐 5000 飞机都不出事儿的概率是几乎一样的

而坐车出事儿的概率有多高呢？我们简单粗暴地测算一下

按照交通部数据，我国万车灭亡率 2.2，也就是平均保有量每增添 1 万辆车，一年就会有 2.2 人死于交通变乱，这还只是 1 年，是 0.022%，按一辆车一年跑 300 天，一次搭载 3 人计较，每坐一次车，发生车祸的概率是 0.0024%。

那坐 / 开 200 次车，不发生车祸的概率是 99.5%；

而这个概率程度，对应到我们前面的表，大要就是 2500 万，玩 5 万次所需要承担的风险。

若是大师有了这个概念，不介入的比例还会这么低吗？相信不会

更不要说，那些擦高层建筑外玻璃墙的、开出租车的、扫大街的、当差人消防的，他们所冒的生命危险，从概率上说，远远高于百万分之一，但他们一辈子都赚不了 2500 万。

我们天天打车、坐地铁、赶公交、炒菜、逛街，这些看似泛泛的勾当，其实都是有必然的概率出人命的，只是这个概率出格出格小，小到我们忽略了

可是就算这些概率再小，也不比百万分之一小几多

然而，你打车、坐地铁、炒菜、逛街一辈子，能赚 2500 万吗？

2500 万什么概念？

500 万的存条目，理财适当就可以衣食无忧（每月躺着拿 1 万元的投资收益）

2500 万的存条目，光理财收益就可以吊打一线城市 95%以上的工薪阶级

2500 万存银行，4%收益率，一年是 100 万，存 3 年就可以在二线城市中间地段全条目买房，若是拿来还房贷，可以支撑 1400 万的房贷，买 2000 万的房子。

上海平均月工资 8000 多，2500 万需要不吃不喝地攒 260 年。

而你需要承担的，只不外是打车 200 次出事儿的风险

一些答本家儿口口声声说，几多钱我都不会拿我的生命恶作剧，拒绝了 2500 万的诱惑

一边天天为了赚几千几万块钱，承受着更高的风险去打车赶公交赶高铁……

若是这么一对比，你还会去做吗？

归正我就想问——这种游戏在哪儿做？？

我能玩到你破产

===============更了个新===========

评论区良多伴侣仍是不太可以或许区分“前提概率”和“自力事务概率”的不同

和大师会商会商挺有意思的，概率学我也没怎么当真学过，友善切磋互惠互利

在这里稍微做一下科普吧，究竟结果高中数学隔太久大师忘失落了也正常

港真，这玩意儿很抽象，且有的时辰反直觉

搞混是常事

但非有一上来殉国正言辞说我错了鄙夷我的……昂……年老你这又是何须……

Overconfidence 也是金融学的大忌好么……

就拿高峻上的伯努利试验（其实就是扔钢镚儿看正背面，伯努利这哥们儿叫的早，所以以他定名，占了个年数大的廉价）来举例吧。

伯努利年老扔了 N 多次硬币后，得出的结论是——不管之前扔了几多次，下一次的概率依然是正面 50%，背面 50%，哪怕前面扔的 1000 次，都是古迹般地正面朝上，第 1001 次扔硬币，呈现背面的概率仍然是 50%。

简单的说，第一次和之后 1 万次、一亿次的扔硬币成果都是互不影响的，每一次扔硬币硬它都有本身的设法，大师是彼此自力的，这是自力事务概率

但我们此刻所要求的，不是自力事务的概率，而是由自力事务构成的持续事务中某个特心猿意马组合发生的概率

这完全就是两回事

这里我们用经典的二叉示范型做一次推导，为了简练，我们只看持续扔三次，可能呈现几多种环境（现实上是因为我懒）

第一次扔，有（正）（反）两种可能，各 50%

第二次扔，有（正，正）（正，反）（反，正）（反，反）4 种可能，这个时辰持续两次为正的概率就只有 4 种中的 1 种，即 25%

第三次扔，已经有了 2 的 3 次方也就是 8 种，别离为（正，正，正）（正，正，反）（正，反，正）（正，反，反）（反，正，正）（反，正，反）（反，反，正）（反，反，反），可以看到，持续三次为正的环境，在 8 种中只有 1 种，可能性是 1/8=12.5%

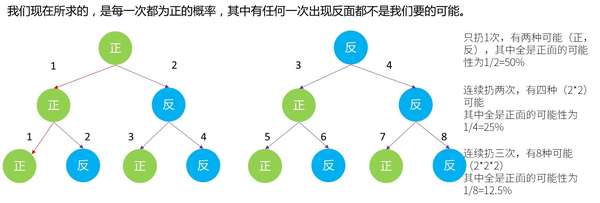
若是恰是生，反是死，那不管是 3 小我同时扔色子都在世，仍是 1 小我扔了三次之后还在世的概率，都是 12.5%

所以自力事务发生的概率不受之前发生的工作成果影响

但当所求的事务概率为一系列自力事务组成的整体事务中，某一前提发生的概率时，就需要叠加前面事务的概率，因为这是这个游戏仍然能继续进行的前提

好比本问题中，要赚 2.5 个亿，那就是持续 5000 次都生还的概率的乘积，中心任何一次，呈现了没有生还的事务，城市让游戏者就地归天。那可能性就只有一种，就是 5000 次都生还，只有第一次，第二次都生还了，才有后续的可能。所以，持续保存 5000 轮，和持续保存 2 轮，存活率天然是纷歧样的。

有的答本家儿很是机智，说，那我玩完 100 次之后，我决议不干，骗一下概率

然后我俄然！决议再玩！概率不就重置变回百万分之一了吗？？

棍骗一时爽，一向棍骗一向爽

可是……你之前玩的那 100 次，固然都活了下来，但每次都堆集了挂失落的概率啊……你之所以玩了 100 次还能棍骗概率，棍骗硬币和伯努利，是因为你命运好玩了 100 次都没挂啊，风险并不会因为没有发生就消弭，也不会因为发生了之后就一路坦途，固然可能有点反常识，但想要棍骗概率，生怕不可。

发表于 2019-04-03 22:13
阅读 ( 805 )
分类：其他类型

可以无偿获得 5000 元，但有 1/100 万的几率当场毙命，你会玩多少次这样的游戏？

你可能感兴趣的文章

相关问题

0 条评论

作家榜 »

推荐文章