图片：O12 / CCO 遥远处所剑星，数学、物理、越野快乐喜爱者

宇宙大爆炸模子是当今被天文学家、宇宙学家、物理学家所普遍承认的关于宇宙成长转变的模子。这个模子的提出是一大群物理学家配合尽力的当作果，并且后来还获得了不竭的修补完美以及持续的验证，可是“宇宙大爆炸”（Big Bang）这个名字倒是由一位极端否决宇宙大爆炸理论的天文学家、物理学家所提出来的，这个物理学家名字叫做弗雷德·霍伊尔。

霍伊尔也是一位卓有进献的天文学家、物理学家，他与福勒等科学家配合提出的元素合当作理论，是诺贝尔物理学奖级此外当作果，但可惜的是，也许是因为与诺贝尔评奖委员会关系严重，1983 年福勒被授予诺贝尔物理学奖，可是霍伊尔没能获奖。霍伊尔在 1948 年与戈尔德等一路创立了“稳恒态宇宙模子”，而且果断否决宇宙大爆炸理论。霍金当初到剑桥读研究生的时辰，就很是想选择霍伊尔作为本身的导师，可惜没有实现。当然，霍金后来反而当作为了推翻霍伊尔稳恒态宇宙模子的主要“推手”。

1949 年 3 月，霍伊尔在加入 BBC 一个会商宇宙发源节目标时辰，嘲讽宇宙大爆炸学说，认为那种学说荒谬的将宇宙的发源付与一场“大爆炸”（Big Bang）。从此，大爆炸（Big Bang）就当作为了宇宙大爆炸学说的代名词，到今天，已经当作为正式的名字了。

任何工作都是一把双刃剑。“大爆炸”这个名字用爆炸来比方宇宙发源与成长转变的理论，确实显得活泼形象，从而在通俗苍生中获得了普遍的普及；可是，因为“爆炸”有着在日常糊口中切当的寄义，从而使得望文生义的吃瓜群众们往往对宇宙大爆炸有着浩繁的曲解。好比，有人认为可以找到宇宙大爆炸当初起爆的那个点，并认为那边就应该是宇宙的中间；有人认为既然是爆炸，那么必然有一个爆炸圈的最外层，认为那边就是宇宙的鸿沟；还有人传闻膨胀的宇宙可以超光速，在知乎上还问出过这样的问题“若是我能抓住宇宙膨胀的边缘，那么是不是我就可以超光速活动了？”；......

所以说，一个名字有时也会带来良多不测的麻烦。宇宙大爆炸理论其实挺复杂，涉及到宇宙从发源到今天的成长演变的全过程，并且有良多尚待解决的问题。今天，我们不谈那么多复杂的工作，而只是谈一件事，宇宙到底是怎么“爆炸”的！

一、一切的“始作俑者”恰是爱因斯坦的广义相对论

在广义相对论呈现以前，我们是没有能力用科学方式去研究宇宙的，那时辰所有对于宇宙的研究都是哲学思虑。一个原因是那时没有足够的不雅测能力，连银河系还看不全呢，当然不领会整个宇宙会是什么样子；第二个原因是没有理论根本，从而无法用科学理论来指导研究宇宙。广义相对论呈现今后，人们终于有了可以在大标准上描画宇宙时空图景的理论。

在研究宇宙之前，人们老是要有一些根基假设，我们称之为“宇宙学道理”。这个道理固然名字很有气焰，可是内容只有一句话：每一时刻的宇宙空间在大标准上是平均且各标的目的同性的。这个假设是如斯的天然，并且也合适我们今天的大标准天文不雅测，从而被认为是宇宙学研究的基石。

可别小看这一句话，这个道理的当作立使我们研究宇宙时候和空间的时辰省了大事儿了。当然，严酷地推导涉及到复杂的微分几何与广义相对论常识。粗略上说来，每一时刻的空间平均意味着我们宇宙四维时空中存在着平均面族（这个“面”指的是四维时空中的三维超曲面），各标的目的同性则意味着存在各标的目的同性参考系，我们再加上一个很是天然的假设，也就是平均面族是独一的，从而可以证实各标的目的同性参考系中任一各标的目的同性不雅者的宿世界线与这个独一的平均面族正交，还可以证实肆意两个平均面之间的各标的目的同性不雅者的宿世界线长度不异。于是，我们可以把这个一族三维超曲面组成的平均面族称为“空间”，把各标的目的同性不雅者的固有时称作“时候”，把各标的目的同性参考系称为宇宙静系，从而一劳永逸的解决了我们宇宙的“时空 3+1”分化问题。【若是没有这个根本，我们在研究宇宙的时辰连如何划分时候和空间可能都难以做到，这是广义相对论中较复杂的一部门常识，与人们日常糊口中自然能区分出时候和空间的感触感染很不不异】

有了上面的根本，我们才能谈论宇宙的春秋、星系间的距离、可不雅测宇宙的半径等等概念，不然时候、空间都是相对的，没有上述根本我们是无从谈起的。

二、三种可能的宇宙空间及其是若何“爆炸”的

在宇宙学道理的根本上，基于微分几何推导，结论是：对于任一时刻，我们宇宙的空间只可能有三种环境——常正曲率空间、平直空间和常负曲率空间。是的，只需要用到宇宙学根基道理，我们就可以获得这样清楚的结论。

不领会空间可能会弯曲的伴侣也许会迷惑，这几种空间到底是什么意思？其实，因为任何空间在极小的规模内都高度近似为平直空间，放在宇宙标准来看，我们人类就糊口在一个极小的规模内，导致人们从起头进行几何学研究的时辰，从没想到过空间还可能是弯曲的。欧几里得在撰写《几何原本》的时辰，把“过直线外一点有且只有一条直线与已知直线平行”作为了一个正义，就是将空间的平直性看做自然当作立的了。无论是欧几里得，仍是后来的很多数学家，都没有熟悉到空间的平直并不是必然的。直到高斯，尤其是其学生黎曼的进献，才让人们知道了，本来空间也可所以弯曲的。

从爱因斯坦的广义相对论颁发起头，人们逐渐加倍理解到，空间不仅仅是可以弯曲的，其实我们糊口的空间和时候（四维时空）真的就是弯曲的。

怎么理解空间的弯曲呢？最好的法子就是站在一个更高的维度上去不雅察低一个维度的空间，这样就很轻易看出其弯曲的特点。好比，球面就是一个弯曲的二维空间，但若是你是一个糊口在球面上的二维生物，你很难熟悉到这一点，而像我们这样糊口在三维空间的生物则相对轻易发现球面是一个弯曲的二维空间。但即使是糊口在三维空间中的我们人类，面临一个庞大的二维球面的时辰，也往往熟悉不清，这样的例子在人类汗青上是真实发生过的，人们直到 400 年前麦哲伦举世航行后，才确信地球是圆的，在这之前，绝大部门人都认为地球是平的。看，固然我们是三维空间中的生物，可是面临一个如斯庞大的二维球面，我们也花了 4、5 千年的时候才熟悉到这个概况是弯曲的（从人类呈现文明算起）。所以，对于一个二维生物来说，几乎没有可能熟悉到他们糊口的二维空间是弯曲的。同样，作为糊口在三维空间中的生物的我们，熟悉到空间是弯曲的，是一个极为了不得的事务，这也恰是爱因斯坦为什么如斯伟大的原因！

1、第一种可能——常正曲率空间

合适宇宙学道理的常正曲率空间其实就是一个平直四维空间（注重不是四维时空）中的三维超球面。这很近似于一个平直三维空间中的二维球面（这个我们通俗人都能理解）。所谓常正曲率，意思就是空间曲率为一个正的常数。这样的空间是一个封锁的空间。

我们知道，在三维直角坐标系（三维笛卡尔坐标系）中，二维球面的方程为

画出来就是一个半径为 R 的球面。同样的，在四维直角坐标系中，三维超球面的方程为

此中的

就是四维空间中的四个坐标值组成的一个点。这个三维超球面我们无法绘制出来，也无法建造一个立体三维模子把它表达出来，因为我们糊口的三维空间中没有第四个维度可以供这个三维超球面来弯曲。

若是宇宙是常正曲率空间，宇宙大爆炸指的就是三维超球面的半径 R 从 0 起头变大的过程！这样，R 就当作为了时候（就是宇宙静系中各标的目的同性不雅者的固有时）的函数，我们一般设

。

我们无法绘制出三维超球面，可是我们可以把这个三维超球面压缩 1～2 个维度来类比，这样也可以让伴侣们对这种环境下的宇宙大爆炸有个感性熟悉。

（1）压缩两个维度来描述

若是把三维超球面压缩 2 个维度，也就是令

，三维超球面就退化为一维的圆周。若是这样的话，宇宙大爆炸的示意动图如图 1。

图 1 把三维超球面压缩 2 个维度，示意宇宙爆炸的过程。

在图 1 这个示意中，那一个维度的圆周就是我们糊口的宇宙，注重这时我们半斤八两于糊口在一条曲线上的一维生物。若是你必然要问宇宙大爆炸的起爆点在哪里，我只能说起爆点在圆心处，可是很遗憾，圆心这个点不在圆周上，换句话说，起爆点不处于我们糊口的空间之中！圆周上被标出的 8 个点，可以认为是宇宙中的 8 个星系，很显然，固然它们本身没有彼此活动，可是他们之间的距离却在不竭增添，这也就是为什么星系之间都在互相远离的原因。

（2）压缩一个维度来描述

若是我们把三维超球面压缩 1 个维度，也就是令

，三维超球面就退化为二维球面。若是这样的话，宇宙大爆炸的示意动图如图 2 所示。

图 2 把三维超球面压缩 1 个维度，示意宇宙爆炸的过程。

在图 2 的示意中，那个球面就是我们糊口的宇宙，这时我们半斤八两于糊口在一个二维球面上的二维生物。同样的，球心作为最合理的起爆点，也不在二维球面上。在这个二维球面上，我们若是朝着一个偏向一向沿直线活动下去，不考虑空间在膨胀的身分，总有一天我们会回到起点，正如麦哲伦举世航行一样。这个特点是常正曲率空间的一个典型性质。所以，固然我们作为三维空间中的生物可以很清晰的看到这个球面在膨胀变大，可是若是是糊口在球面上的二维生物们，显然是不会发现本身所糊口的空间存在“鸿沟”的！

（3）不压缩维度来描述

因为我们无法绘制三维超球面，所以很遗憾，这时辰我们画不出图来了。为了更好的理解这种宇宙空间的特点，可以给出三维超球面中的两个事实，会对想象这样一个四维空间中弯曲的三维超球面有一些帮忙：

事实 1 ：与二维球面一样，在三维超球面中，若是我们朝着任一个偏向一向沿直线活动下去，不考虑宇宙的膨胀，总有一天我们会回到起点。关于这一点，我无法绘图表达，大师可以自行脑补，或者用低维度的环境做参考。

事实 2 ：在二维球面上，若是我们绘制一个圆周，这个圆周其实会有两个圆心和两个分歧的半径，如图 3 所示；同样的，在三维超球面上，若是我们绘制一个球面，这个球面也有两个球心和两个分歧的半径，如图 4 所示。

关于事实 2 乍一听到不轻易理解，我这里多诠释下。先说二维球面，图 3 中的以 O 为球心的二维球面上绘制一个圆周（橙色虚线圆周），在我们三维空间中的人看来，这个圆周的圆心当然在点 K 处，半径为 KC=r，可是别忘了，点 K 不属于二维球面。所以，在二维球面上的二维生物看来，这个圆周的圆心既可以在 E 点，此时半径为“圆弧 EC”（橙色实线圆弧）；圆心也可以在 F 点，此时半径为“圆弧 FC”（绿色实线圆弧）。可见，弯曲的二维球面上的圆周，半径很大之后，圆的周长反而可能很小。

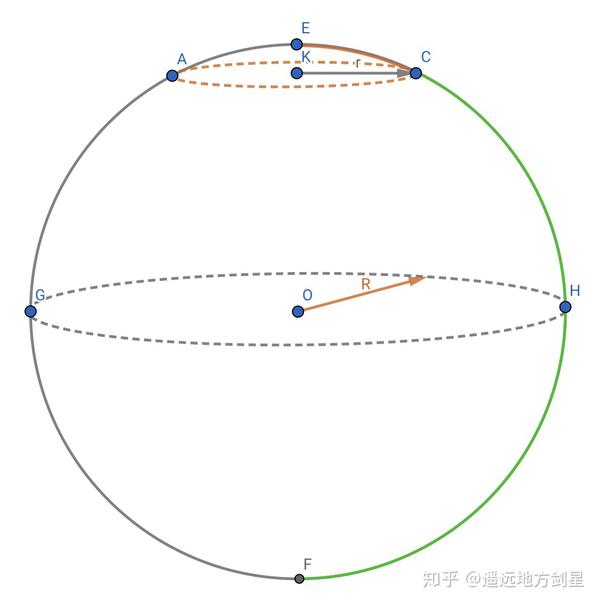图 3 二维球面上的橙色虚线圆周其实有两个圆心 E 和 F，有两个半径“弧 EC”和“弧 FC”

回到我们糊口的三维空间，若是我们的宇宙确实是常正曲率空间的话，也会有近似的现象。如图 4 中以 A 为球心绘制一个半径为 r 的球面，点 C、P、D、Q 都是球面上的点。那么在我们的宇宙中必然存在着别的一个点 S，这个点到球面上各点的距离也都一样，只不外这个距离可能会很大。图 4 只能是一个示意，因为我们无法画出真实的环境，原因是我们空间的维度不敷。

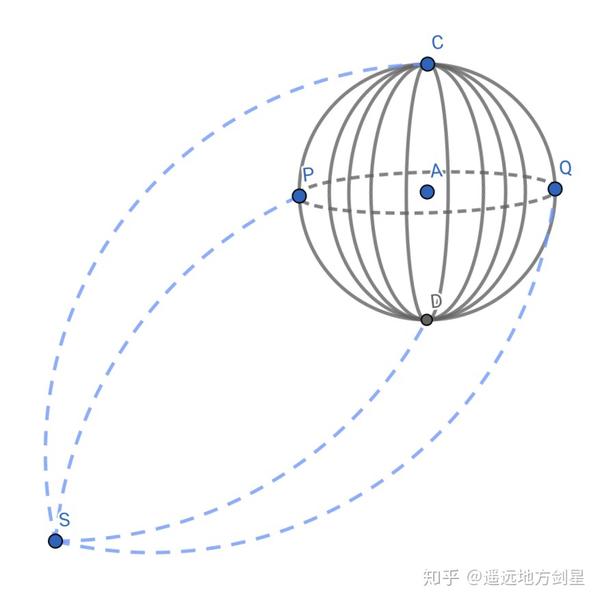图 4 在三维常正曲率空间中绘制一个以 A 为球心、AC=r 为半径的球面，那么空间中也必然存在别的一个点 S 也是这个球面的球心，S 到 C、P、D、Q 等球面上个点的距离 R 也都相等，只不外若是 r 很小的话，R 会很大。

换个更形象的说法，当我们捧着一个地球仪的时辰，我们本身认为这个地球仪的球心在我们手的掌控之中，可是若是我们的宇宙是常正曲率空间的话，我们就应该知道，在很遥远的处所必然存在着别的一个点，这个点也是你手中地球仪球面的球心，并且相对这个球心来说，你手中的地球仪球面半径大的惊人，起码跨越 460 亿光年，甚至可能跨越 1000 亿光年。

2、第二种可能——平直空间

这种可能是最简单的一种环境。在这种环境下，我们的宇宙就是一个尺度的平直欧几里得三维空间，只不外处于膨胀过程中。固然在不竭膨胀，可是任一时刻，我们宇宙的空间都是平直的三维欧氏空间。压缩一个维度后，这种宇宙大爆炸的示意动图如图 5 。

图 5 压缩一个维度后，平直空间宇宙大爆炸示意动图

伴侣们可能会有疑问了？图 5 示意的哪像大爆炸啊？不就是一个平均的平面被平均的拉伸吗？为领会释这种环境下的宇宙大爆炸，我们不得不请出宇宙学研究中最根本的“罗伯逊 - 沃克”度规（RW Metric）。这个宇宙的线元长度表达式如下，

上式第一个等号右边是用平面直角坐标系暗示的，第二个等号右边是用球坐标系暗示的，但本色都是一样的。最关头的一点是空间线元前面的系数

。在前面介绍第一种环境常正曲率空间的时辰，我们提到了

就是三维超球面的半径。可是在第二种环境中，

不再有这样的寄义，它只是一个随时候转变的系数罢了。

问题是这个

在

时，

。从而我们可以计较获得，

的时刻，空间线元长度恒为 0 。这也就意味着 t=0 这个时刻没有空间。可是，只要

，不管

此时是何等小的正数，空间线元就笼盖了全数的三维坐标，当作为了一个无限大的三维欧氏空间。从这个意义上讲，这种环境下的宇宙大爆炸只是在

这个奇点处宇宙空间才不存在，只要一起头“爆炸”，无限大的三维平直欧氏空间就降生了。所以，我们的示意图只能是这个样子啦。

这种环境下，连疑似的起爆点我们都找不到，看到的就是一个无限大的三维欧氏空间在不竭膨胀罢了。

3、第三种可能——常负曲率空间

我们泛泛很少接触负曲率空间，所以对于这种环境可能更不熟悉。这种环境下，宇宙的任一时刻，空间都曲直率为负的常数的弯曲空间。这种负常数曲率空间其实就是平直四维空间中的三维超扭转双曲面，可以类比为平直三维空间中的二维扭转双曲面。这种负曲率空间并不封锁，是一个开放的空间。

二维扭转双曲面的方程为

近似的，三维超扭转双曲面的方程为

同样因为维度的原因，我们无法画出这种三维超扭转双曲面的样子。仍是近似第一种环境，经由过程压缩维度，来给大师一些感性熟悉。

（1）压缩两个维度来描述

若是令

，获得的方程很简单，就是一条双曲线。我们知道双曲线分为互不连通的两部门，我们只取

的部门，因为此时这条双曲线就代表了我们糊口的一维空间，而我们显然只能糊口在连通的空间中，另一条不连通的曲线与我们没有任何干系。

此时的宇宙大爆炸其实就是

从 0 起头增大的过程，这种环境下的

，看起来的样子如图 6 。

图 6 常负曲率空间压缩两个维度后，宇宙大爆炸示意图。

请注重，在

的时辰，双曲线退化为两条

角的折线，也就是

的图像。所以，这种环境下的宇宙大爆炸，其实是从两条折线所代表的一维空间起头膨胀的过程。当然，空间是两条折线的时辰，折点处的空间是持续但不成导的，这种空间也同样是不成理解、不该存在的，所以，这也是大爆炸奇点可能的一种形态。

跟着空间的膨胀，整条曲线还沿着

轴在上升。可是，要知道，

坐标轴是一个我们无法触碰的维度，所以，作为糊口在这条曲线上的一维生物，我们无从感知曲线在某个其它维度的上升。可是，曲线上标准的膨胀仍是显然的，这丛所标心猿意马的多个点逐渐在分手就可以感触感染到了。

（2）压缩一个维度来描述

近似的，若是压缩一个维度，令

，三维超扭转双曲面就退化为二维扭转双曲面。这时宇宙大爆炸的动图如图 7 所示。

图 7 常负曲率空间压缩一个维度后，宇宙大爆炸示意图。

这种环境下的宇宙大爆炸是从一个圆锥面起头的，“起爆点”，也就是大爆炸奇点，是一个无限大的圆锥面。这种环境下，若是我们固心猿意马

，获得的

平面（这显然是一个与

坐标面平行的平面）与扭转双曲面的交线是一个半径为

的圆周。所以，我们也可以认为，这个双曲面是由无数条这样的圆周在

维度上移动组合而当作的。

（3）不压缩维度来描述

这下可难了，我们即画不出图来暗示真正的三维超扭转双曲面，也没法举出太有用的有助于理解的例子。参照压缩一个维度的说法，也许可以这样想象这种空间：

固心猿意马某一个

之后，获得的

三维超平面（这个三维超平面其实就是四维欧氏空间中的某一个三维欧氏子空间）与这个三维超扭转双曲面订交获得的二维曲面是一个半径为

的球面，可是要注重，这个球面的球心却不在我们所处的三维超扭转双曲面空间之内。那么，我们这个三维超扭转双曲面空间其实就是由无数个这样的球面在

维度上移动组合而当作的。

嗯，作为三维空间中的生物，硬要去想象四维空间中的场景，难度是很大的。有的人甚至说这是不成能的。说真话，我也想象不出这样的三维超扭转双曲面到底是什么样子，因为我们都从来没有过第四个空间维度的体验。所以，最后只能经由过程数学计较来理解这些抽象的概念了。

三、关于宇宙大爆炸的几个问题

有了上面描述的根本，再往返答下面的一些问题，就相对轻易了些。

1、宇宙有中间和鸿沟吗？

谜底是——没有。

这其实从宇宙学道理就可以获得。宇宙学道理告诉我们，任一时刻的宇宙都是平均的和各标的目的同性的。那么显然，若是有中间，或者有鸿沟，都意味着在宇宙中存在一些位置比其它位置更特别，这当然是违反宇宙学道理的。所以，这个问题的谜底很是明白。

多说一句，在第三种环境“常负曲率空间”下，似乎那个压缩一个维度后的扭转双曲面有一个中间啊？但那只是我们站在更高维度上看到的一种情境，而作为身处二维扭转双曲面内的二维生命来说，它们是感触感染不到存在中间的。这是因为对曲面上任一点，都存在着这样一种等度规的映射，对这个点来说是恒等映射，可是却可以让这个点的任一矢量扭转任一要求的偏向和角度。仍是那句话，只有经由过程数学计较，才能理解这些抽象的性质。

2、大爆炸奇点到底是什么？

谜底是——可能是一个点，也可能是一个不成导的无限大空间。

这显然取决于我们的宇宙到底是三种环境中的哪一种。对于第一种环境，可以认为是一个点，或者认为是一个半径无限小的三维超球面；对于第二种环境，可以认为是一个点，也可以认为就是一个无限大三维欧氏空间；对于第三种环境，只能认为是一个不成导的无限大三维退化超扭转双曲面。

但不管怎么样，都可以经由过程某种坐标转变，把大爆炸奇点变换当作为一个三维类空超曲面。所以，万万不要再把大爆炸奇点简单地舆解为一个点了，其实大爆炸奇点和我们凡是意义上的一个点很不不异。

3、宇宙巨细有限吗？

谜底是——可能有限，也可能无限。

这也取决于我们的宇宙到底是哪种环境。

第一种环境下的宇宙体积是有限的，我们可以经由过程微分几何计较获得这种三维超球面的体积，成果是

。显然，跟着宇宙的膨胀，

的增加，宇宙的体积也会增加。当然，宇宙是否会永远膨胀下去，这还需要进一步研究。

第二种环境和第三种环境的宇宙空间都是开放的，不封锁的，显然体积是无限大的。

可是不管宇宙体积是否有限，宇宙必然都是无中间、无鸿沟的。

4、为什么会有可不雅测宇宙与不成不雅测宇宙的区分？

这个问题本文篇幅有限，只能简单申明一下。

起首，宇宙大爆炸刚起头的时刻，物质和能量堆积在一路，处于超高温度、超高压强下，光子是无法自由穿梭的。也就是说，在宇宙大爆炸起头后的一段时候，宇宙是不透明的。大要从宇宙大爆炸发生 40 万年后，光子退藕（退出耦合的意思），宇宙才被认为是透明的。这个时辰某些位置的光子颠末很长的时候，终于跑到了我们今天的视野里，这被认为是我们可以或许看到的最早的光子。我们知道宇宙的春秋大要是 137 亿年，那么这些到我们眼里的最早的光子显然奔驰了 137 亿年（一起头那 40 万年太小，就忽略不计了）。可是，跟着宇宙的膨胀，那时这些光子发出时刻的位置今天已经膨胀到离我们更远的处所了，我们所说的可不雅测宇宙的半径，指的就是这些光子发出时刻的位置今天离我们的距离，颠末复杂的计较，人们估量它们今天离我们大要 460 亿光年。这就是可不雅测宇宙半径在今天的值。跟着宇宙的膨胀，跟着时候的增加，可不雅测宇宙半径还会转变。今朝看来，显然还会继续变大；至于最终会如何演变，这取决于我们宇宙到底是哪种空间景象，又是若何继续膨胀的，这是一个需要深切研究的课题。

5、到底宇宙是三种空间中的哪一种呢？

谜底是——这个问题现在还没有切当谜底。

可是我们可以有一些猜测。按照宇宙学道理和爱因斯坦广义相对论的推导，我们可以获得一个宇宙学的恒等式，

，此中

，

是当今的哈勃常数（其实就是我们前面说的函数

在当今时刻的值），

是万有引力常数，

是当今时刻宇宙中物质的密度，

是当今时刻宇宙中辐射的密度，

就是赫赫有名的宇宙学常数（就是我们今天也米有搞清晰的暗能量的来历，有时也叫做真空能量密度参数），

就是

在当今时刻的值，

则是用来标识我们宇宙到底是三种环境中的哪种的指标，

代表常正曲率空间，

代表平直空间，

代表常负曲率空间，

只有这三个取值。

宇宙学家和天文学家按照大量不雅测，估量出了上面除了

以外的其它参数，固然有些很不切确，可是带入上面的恒等式获得的成果似乎表白，

接近 0 。也就是说，我们可以按照今朝不雅测成果猜测，我们的宇宙在大标准上很可能是平直的三维欧氏空间。

当然，除了这些不雅测，我本人还甘愿答应给出别的一种猜测。那就是，究竟结果三维以上更高的维度我们谁都没有见过，若是利用奥卡姆剃刀，“不增添没有需要的实体”，那么我们可以猜测原本就没有第四个空间维度。从而，我们也许可以认心猿意马

，宇宙在大标准上就是一个平直的三维欧氏空间。当然，这是我本人的痴心妄想，仅供参考，万勿当真。

 

宇宙就是这样爆炸的，不要再去探寻宇宙的鸿沟、宇宙的起爆点了，我们的宇宙也许是一个有限而无界的空间，更大的可能是一个无限而无界的空间。我们人类糊口在此中，细微的连一粒尘埃都远远算不上，可是，我们人类伟大之处在于，我们知道这个宇宙可能是什么样子的，这也许是宇宙赐赉我们人类最大的幸福！