一壶烧开的水从多高倒进嘴里不会觉得烫?

 知乎用户,云行雨施,品物流形
知乎用户,云行雨施,品物流形
先说结论:大约50米摆布。
水从高空落下,先倒的水快,后倒的水慢,所以必然很快扯破,当作为藐小的水滴。
是以,这里就只会商水滴的散热问题,而不考虑一大团水的散热。因为这种环境更为常见,计较也更为简单。
本着物理学「真空中球形鸡」的思维体例,这里考虑球形小水滴。因为水滴在高速下落,所以其四周空气的温度,其实可以视为不受水滴影响。这种近似有其物理按照——在低温物理中,人们经常用低温流体为物体降温、连结温度,可以使物体温度的浮动降到很低。
又为了更进一步的简化,这里将水滴视为两层——内层和外层:
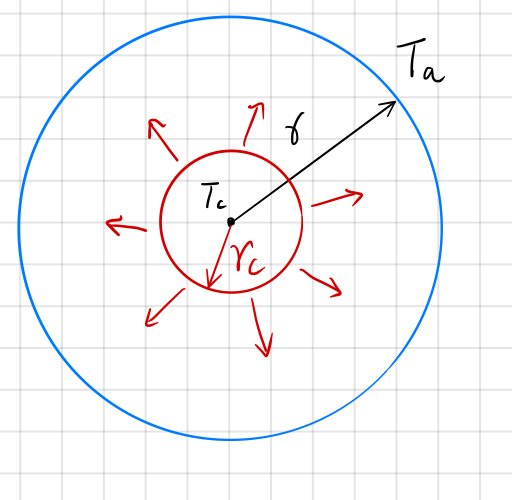
内层的半径为 ,而外层的半径为
。因为内层很小,所以假设温度平均。而外层之中的传热,则视作近稳恒传热,合适能量输入、输出相等的原则。
这个假设当然不严酷合适现实,但可以连结数学上的简练。最终的成果,也不会与真实数值相差甚远。
所以,这里外层的温度合适这样的形式:
其图像是这样的:
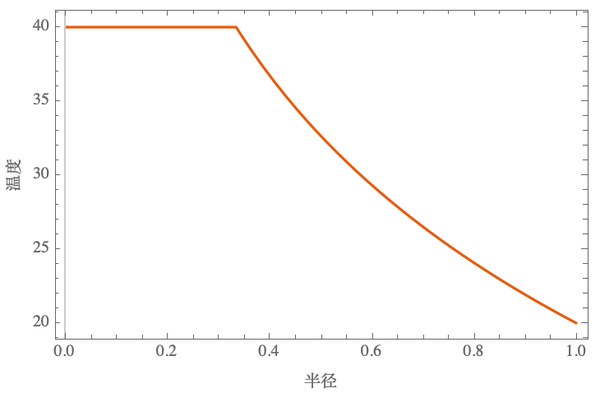
真实的温度分布当然不是这样,这里做了近似。但误差不会很大。后面我们会看到,内层的巨细,对于成果影响不大。
经由过程上式,轻易求的内层散热的速度:
据此,可以获得内层温度随时候转变的函数:
此中, 即开水温度,为100摄氏度,
为空气温度,这里设心猿意马为20摄氏度。c是水的比热,k是水的热导率,
是水的密度。
如斯,即可绘制水滴焦点温度随时候转变的图像:
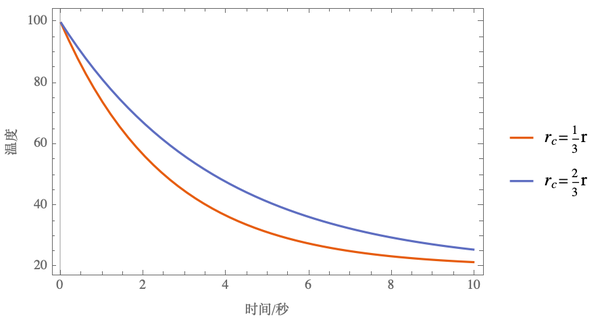
可以看到,若是水滴半径为3mm,那么,不外五六秒,水滴的焦点温度就已经可以进口了。到了十秒,温度就接近空气了。并且,非论拔取焦点半径是几多,其曲线的不同都不太大。这里可以认为,平安时候大约是5秒。
水淌下落时,因为空气阻力的影响,其最终速度,大约在9~13m/s之间。这里为了简单,取10m/s。而雨滴要加快到这一速度,只要1秒。
取平安时候来计较水滴的高度,获得的高度是50米。也就是说,大约五十米的高度,就足以闪开水冷却到平安的温度了。
- 发表于 2019-04-29 21:14
- 阅读 ( 833 )
- 分类:其他类型
你可能感兴趣的文章
- iPhone苹果手机如何取消订单退款 2549 浏览
- 進擊的巨人第三季part2在哪看,怎么在线看进击 998 浏览
- cdr如何制作天蝎座图标 736 浏览
- 怎样在QQ空间农场中将普通摊位升级到第5级 874 浏览
- 谷歌浏览器怎么删除某个cookie 921 浏览
- 女性40以后饮酒对身体的影响 826 浏览
- 如何对Word中的表格数据快速求均值 876 浏览
- 在PPT中让文字逐条显现 815 浏览
- p使用pr的小技巧-2 768 浏览
- Office2013官方正式版免费完整下载安装激活教程 806 浏览
- 吃完大蒜嘴里有味儿怎么办怎样去除口臭味儿 1046 浏览
- PR 做一个黑白世界的效果 969 浏览
- 怎么查看Delphi软件中控件的属性及代码 821 浏览
- 如何查看电脑处理器(CPU)的详细参数 1048 浏览
- 吃西葫芦对你身体有哪些好处 820 浏览
- photoshop使用内容识别删除选中区域 1253 浏览
- 如何快速找出excel两列数据的不同项 1146 浏览
- win8系统如何禁止特定指定软件程序联网 975 浏览
- MATLAB画图标记特殊点的方法 2230 浏览
- 图解利用WPF创建一个全屏应用程序 760 浏览
- Excel技巧之——去掉数据透视表中的“空白” 3067 浏览
- 采用MATLAB画一个分段函数图像的方法 1189 浏览
- word中输入某个字后显示的是其他内容该怎么办 1092 浏览
- chemoffice 2018 如何激活 1327 浏览
- 如何从百度云上下载视频到电脑中 988 浏览
- WPS怎么给表格行添加背景色 1041 浏览
- Word如何设置编辑内容 955 浏览
- BIOS退不出怎么办 1652 浏览
- WPS怎么插入表格 1125 浏览
- word插入图片后只显示空白框该怎么办 2604 浏览
相关问题
0 条评论
0 篇文章
作家榜 »
-
 xiaonan123
189 文章
xiaonan123
189 文章
-
 汤依妹儿
97 文章
汤依妹儿
97 文章
-
 luogf229
46 文章
luogf229
46 文章
-
 jy02406749
45 文章
jy02406749
45 文章
-
 小凡
34 文章
小凡
34 文章
-
 Daisy萌
32 文章
Daisy萌
32 文章
-
 我的QQ3117863681
24 文章
我的QQ3117863681
24 文章
-
 华志健
23 文章
华志健
23 文章
推荐文章
- 怎样才能拍摄出好看的婚纱照
- 新生儿姓名重复人数怎么查询
- 微信怎么解除绑定的手机号码
- 携程上怎么领取优惠券
- 微信账号如何进行申述找回
- 微信怎么制作电子名片
- 微信里的音频文件怎么收藏保存
- 如何查看微信账单
- 微信听筒模式如何切换回来
- 怎么在微信里查询社保信息
- 微信怎么把收藏的内容分享到朋友圈
- 斗鱼直播怎么联系客服
- 微信怎么设置不让别人加自己
- 微信里的聊天记录如何打包发给别人
- 怎么更换微信绑定的手机号
- 美颜相机怎么去除水印
- 王者荣耀如何让别人看不到战绩
- 微信如何查看实名认证信息
- 手机阿里巴巴怎样使用以图找货功能
- 微信保存的图片在哪个文件夹里
- 华为手机计时器功能怎么使用
- 快手上怎么卖东西
- 苹果手机自动删除软件怎么办
- 怎样最低的价格买到心仪的手机
- 苹果xsmax怎么设置动态壁纸
- 百度手机卫士如何关闭软件锁
- iphoneX屏幕怎么分辨原装
- 微信如何设置支付时验证身份
- 微信聊天联系人为什么多了耳朵标志?如何关闭
- 微信支付如何设置亲情卡